Die herkömmlichen Berechnungen über das Potenzial einer geladenen Kugel oder Hohlkugel gehen zwar ebenfalls von einer ,,Gleichverteilung” der Ladung (oder Masse) aus, jedoch im räumlich- quantitativen Wortsinn, weshalb die Hinzunahme einer gegensätzlichen Ladung im Innern zu völliger Kräfteneutralität gegenüber einer äußeren Ladung führen muss. Insofern ist dies der falsche Ansatz!
Für Interessierte hier ein Link : Die Feldfreiheit des Kugeldipols (aus der klass. Potentialtheorie)
Das Elektron als feste Ladungsquantität mit Eigenvolumen lässt sich jedoch als Ganzes nicht weiter räumlich verteilen, es ist höchstens mit gleicher Wahrscheinlichkeit (Schrödinger) zwar ,,wolkenähnlich” , aber offenbar doch als ganzes, vollständiges Eigenvolumen überall in der atomaren Kugelfläche oder anderen Formen von Orbitalen zu finden , wirkt also auf eine äußere Probeladung über die Zeit gesehen aus verschiedenen Richtungen ein, etwa wie ein um sein positives Ende statistisch herum rotierender Dipol, und hat deshalb letztlich keine abschirmende Wirkung auf das Kernpotential.
(Dies gilt auch für die Vorstellung, bei der sich im Zuge der sog. 2. Quantisierung eine umlaufende Trajektorie durch eine statistische Vernichtung und Neuerzeugung des Elektrons mittels einer Wahrscheinlichkeitsfunktion zusammensetzt.)
Um eine Abstraktionshilfe zum Verständnis des Modells zu geben, wird zuerst die Konstellation ,,Atom mit äußerer Punktladung” erläutert:
Man stelle sich vor, eine Punktladung im Kosmos zu sein und man habe eine Druckfeder in der Hand, die in einiger Entfernung zu sich eine gleiche Ladung auf Distanz hält. Gleichzeitig hält man eine zweite gleichstarke Zugfeder hin zu einer um diese Ladung statistisch herumlaufenden gegensätzlichen Ladung, deren zeitlicher Aufenthalt auf der Kugelfläche gleich verteilt ist, und deren Fluchtversuch bei der Rotation auch durch eine Zugfeder zum Zentrum hin unterbunden wird. ( Ein ruhendes System dieser Anordnung würde sich zu einem Dreieck kompensierter Kräfte einstellen, aber der Vergleich hinkt insgesamt ein wenig, denn die Zugfeder müsste bei größerer Dehnung hingegen kleinere Kraft liefern, was am hieraus entstehenden zeitlichen Mittelwert der Kraft jedoch nichts ändert.)
Nun gibt es bei kugelhafter oder auch andere symmetrische Bewegungen auf beiden durch die Äquatorialebene getrennten Halbsphären aus jeder Richtung betrachtet zwei Punktmengen, deren Elemente je ein Gegenelement mit inversen Koordinaten zueinander bezüglich des Mittelpunktes haben. Infinitesimal gesehen bleibt nur der Äquator selbst übrig, er gehört als Randwert auch zur Ebene, alle anderen Punkte haben ein Pendant, deren Mittelwert die GEDACHTE(!) Ebene für die mittlere Kraft erzeugt. Der Mittelwert dieser Ebene liegt dann schließlich im Zentrum, und zwar aus jeder Richtung betrachtet. So hat die von mir ausgehende Zugfeder eine im Zeitmittel verkürzte mittlere Länge (= Kraft) , die ohne ,,Seitenkomponente” ins Kugelzentrum weist. Zeitlich gesehen wird so meine mittlere Kraft, deren Einheitsvektor entlang des Äquators gleichbleibt, hierdurch effektiv verringert, während die Kraft zwischen mir und der ,,ruhenden” Zentralladung gleichbleibt.
Die Kräfte zwischen innerer und außen rotierender Ladung als ,,quasifreies” System sind zeitlich kompensiert und unterliegen außer einer geringen Schwingung um den gemeinsamen Schwerpunkt keiner Störung, und infolge der Kernträgheit wird sich das Zentrum eines solchen Gebildes kaum bewegen. Durch die nun im zeitlichen Mittel vermindert erscheinende Anziehung zum umlaufenden Elektron würde man sich (hier als Proton angenommen) gegen das vollständige Atom mit einen winzigen Überschuss in der Kraftsumme auseinanderbewegen. Als Elektron jedoch würde man zum Atom hin (oder auch jeder Materie gegenüber) insgesamt eine leichte Anziehung erfahren, da nun eine abstoßende Teilkraft vermindert ist.
Soweit das Gedankenexperiment.
Auch für punktsymmetrische Orbitale müssen diese Verhältnisse im Zeitmittel aus jeder Richtung betrachtet gelten.
Da die Federn in Wirklichkeit mit 1/R^2 nichtlinear sind, wird die gedachte Äquatorialebene im atomaren Nahbereich gekrümmt ausfallen, das Kraftmittel also um eine Ordnung höher verfälscht, jedoch wird dies in 5-6 Atomradien Entfernung bereits unerheblich. (Die R-Abhängigkeit von F wird hier allgemein vernachlässigt, muss neben magnetischen Effekten im Nahfeld jedoch als Zusatzvariable beachtet werden, da diese Kraftfunktion im Nahbereich dekomprimiert und in der Quantentheorie ihre korrigierten Lösungen findet.) Insofern bleibt diese Abschätzung weiterhin eine Näherung, aber für die Gravitation selbst ist sie mehr als ausreichend genau, denn diese entsteht sozusagen als abstandsbezogene Fortsetzung quantenmechanisch berechneter Kraftverhältnisse erst außerhalb der Atome.
(Die aktuellen Aussagen französischer Physiker gehen dahin, dass magnetische Effekte trotz des großen Abstandes zum Gravitationszentrum der Erde ortsbezogenen Einfluss auf den Zahlenwert von G schon ab der zweiten Nachkommastelle haben sollen. Es ist jedoch wahrscheinlich, dass diese Schwankungen von experimentellen Abstandsunterschieden zum Erdmittelpunkt dominiert werden.)
Stellt man nun zwei vollständige gleiche (oder auch verschiedene) Atome gegenüber, so ergibt sich nach der beschriebenen elektrischen Kräftesummierung ein winziger anziehender Überschuss, den wir als Gravitation wahrnehmen, und im Massenkollektiv multipliziert sich diese Erscheinung dann sinngemäß, woraus sich als Konsequenz das Newton’sche Gesetz und die Gravitationskonstante herleiten lässt.
Es muss betont werden, dass es sich hierbei NICHT etwa um einen winzigen Ladungsüberschuss handelt, sondern um eine aus elektrischen Vektorfeldern zwischen atomaren Ladungen geometrisch erzeugte Kraftdifferenz, die man als ,,Pseudofeld skalaren Charakters” bezeichnen könnte , das keine ausgeprägte Richtung besitzt, und sowohl um die Zentren der beteiligten Atome als auch um daraus gebildete Massen herum Äquipotentiallinien aufweist. Dies hat selbst bei Fachleuten meist zur Fehlinterpretation der Rechnungen geführt! Neu hierbei ist die Verrechnung des Zeitmittels als ,,unorthodoxe Variante”, ein lange bekanntes Kraftergebnis über die Atomradien mit dem Erdradius als Abstandsreferenz zu bestätigen.
Die Proton- Proton- Wechselwirkung wird hier quasistatisch betrachtet, während die Berechnung der Elektron- Proton- Wechselwirkung über den experimentell bekannten Atomradius rA auf einen winkelabhängigen Mittelwert führt. Der bei der Kräftesummierung zweier Atome verwendete Wahrscheinlichkeitsradius rB jedoch, unter dessen Winkel alle bewegten Elektronen wechselwirken, ist nur unter Aspekten einer Relativbewegung zueinander über das quadratische Mittel berechenbar.
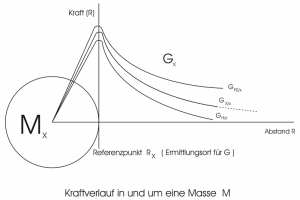
Der entstehende Kraftverlauf um kugelförmige Massen herum ergibt sich aus der Summierung aller beteiligten atomaren Kraftkurven über die gesamte Ausdehnung des Kontinuums (= Massenanhäufung, nicht zu verwechseln mit Raumzeit- Kontinuum!) hinweg. Berechnungen dieses integralen Gesamtfeldes kugelförmiger Körper befinden sich ebenfalls noch im Versuchsstadium. Der abstandsbezogene differentielle Kraftverlauf um den Körperschwerpunkt herum (Gradienten) findet dann in den bis heute hypothetisch gebliebenen höherdimensionalen ,,Raumzeit- Krümmungswerten” der ART seine Entsprechung. Da sich die Eigenschaften der atomaren Kraftfunktion bei Massen einer spezifischen Atomsorte auf den räumlichen Gesamtverlauf der Kraftverteilung um den daraus gebildeten Körper herum isomorph als ,,Kennzeichen” übertragen, muss sich bei Annäherung mit einer bekannten ,,Eichmasse” z.B an einen Planeten und durch Vergleich des differentiellen Kraftverlaufs aus einem (noch zu erstellenden) Katalog aller möglichen Elementekombinationen eine Aussage über die Zusammensetzung des Planeten ableiten lassen.
Die am Übergang zwischen Massekugel und Umgebung entstehende Unstetigkeitsstelle für die Kraft wird durch Verwendung von Gx als Funktion der Abstandsvariablen dort nun differenzierbar und gestattet einen stetigen Übergang z.B. des Potenzials zwischen zwei H-Atomen zu Newton’s Law in größerer Entfernung.
Hierzu ein Link, der jene klassische Nichtdifferenzierbarkeit behandelt (Abb. 4.7) : Aus der klass. Potentialtheorie
Interessante Zusammenhänge ergeben sich aus folgender Publikation : Gravitation und Feinstrukturkonstante (R. Cahill)
Allgemeine Betrachtung :
Die universell so entstandene Gravitationsenergie entstammt eigentlich der gesamten Arbeit bei der Trennung der Atome aller Materie, und sie kann seit dem Einsetzen des kosmischen Kondensationsprozesses (und später in Materieform) letztendlich nur noch durch Reibung beim Bremsen des Gravitationsvorganges bzw. durch Falldeformation in Wärme umgesetzt werden. Dieses Schicksal erleiden auch alle sogenannten ,,Virtuellen Arbeiten” (z.B. statisch bestimmt gestützte Massen), die irgendwann wieder auf das kleinstmögliche Potenzial ,,herunterfallen”, ganz gleich auf welche Weise.
Das urzeitlich entstandene ladungsbedingte Gesamtfeld aller atomaren Materie, das eine geometrisch erzeugte und elektrisch kompensierte Restkraft in dieser speziellen Form hervorbringt, trägt neben seinen ,,lichtneutralen Äthermerkmalen” auch eine konstante universelle Gesamtladung, und eine Feldstärke- bzw. Kraftänderung zwischen Atomen oder Materie kann nur noch durch Variation des Abstandes bewirkt werden, wobei keine schwingende elektrische Energie übertragen wird und sich die Kraftwirkung nach einem pseudostatischen Prinzip der Energieübertragung instantan bemerkbar machen muss, – ein denkbarer Unterschied zur Ausbreitung von Wellen!! (Gravitation überträgt demnach keine Wirkung, die zur Ausbreitung Zeit braucht, sondern war und ist sofort vorhanden, seit die ersten beiden Atome entstanden waren.) (Siehe Link zum paper von W. Engelhardt)
Zusätzliche Anmerkungen zum Verständnis der Rechnungen :
Wichtiger Hinweis : Die numerische Behandlung der Modellformel ist nur mit einem Rechenprogramm möglich, das mindestens 100, besser 500 Nachkommastellen verarbeiten kann! (Taschenrechner können dies in der Regel nicht leisten.)
Die Proportionalitätskonstante in (5) entsteht bei Verwendung von G. Sie sagt primär aus, dass die Gravitationskraft , zumindest bis auf molekulare Distanzen, um diesen Faktor konstant kleiner ist als die elektrische Kraft – eine alte Feststellung, nur hatte bislang niemand eine Erklärung dafür.
Gx hat abhängig von R, rA und rB den Graphen wie im Maple- Plot dargestellt. (Er zeigt im Grunde auch, welchen Wert die Gravitationskonstante bzw. das Verhältnis von gravitativer zur elektrischen Kraft für uns, z.B. auf dem Mond ermittelt, angenommen hätte, wenn wir für R den Mondradius nehmen.) Mit dem festen Wert für R= Erdradius sowie den festen Atomradien der beteiligten Elemente erhalten wir so den Wert 0.81E-36, der dann für unser Maßsystem als Faktor in der Gravitationskonstanten G enthalten ist, diese festlegt und ebenfalls bis auf ganz kleine Abstände ,,konstant” erscheinen lässt.
Der Wert der Gravitationskonstanten hängt also neben der verwendeten Masseneinheit vorrangig von ihrem ursprünglich gewählten Ermittlungsabstand zum Bezugsmassenzentrum ab (normierte Anziehungskraft des Urkilogramms in Newton) und legt so das Verhältnis zur elektrischen Kraft fest, welches dann ein Teilfaktor von G selbst wird.
Die mit der Modellrechnung erweiterte Coulombkraft in (4) sagt nun schon auf der Basis von nur zwei beliebigen Atomen durch Gx, warum dies so ist, (5.1) ist nur der numerische Nachweis dafür, und zeigt zumindest bis zu Entfernungen von 10E20 Metern (Grenze des verwendeten Rechenprogramms und womöglich auch des Universums) agenähert quadratisches Verhalten.(Siehe Abschnitt Pioneer-Anomalie) In Atomnähe dekomprimiert diese Funktion jedoch und nimmt im Wesentlichen die Form des sog. Coulombwalls an, wobei eine Ähnlichkeit etwa zum Lennard-Jones-Potential, der Potentialkurve zweiatomiger Moleküle oder angenähert zur Van der Waals – Kraft offensichtlich ist.
Zum Problem freier Neutronen :
April 2010 : Erste Ergebnisse führten zur ,,Tripolvariante” der Nukleonen;
Siehe Essay zur starken Kernkraft (PDF, Downloadsektion)
Interessante experimentelle Ausblicke gibt folgender Link : Ultrakalte Neutronen
Auf ein Kontinuum erweitert (erst dann spricht man ja erst wirklich von ,,Masse”) ergibt sich automatisch Newtons Gesetz einschließlich der Gravitationskonstanten G, in welcher das atomare Gx bereits als Faktor steckt, und so diese Kraftfunktion auch auf den gravitatorischen Kraftverlauf zwischen rellen Massen abbildet. Somit enthält G schon diese ,,neutralisierte Spezialform” der elektrischen Kraft, weshalb sie sich dann zwangsläufig einer Vereinigung ,,mit sich selbst” widersetzen muss.
Implizit ergibt sich dadurch: Da Proton und Elektron zwar gleiche Ladungsmenge, aber weitaus verschiedene Massen haben, muss ,,Masse” atomar wie Nuklear betrachtet eine ,,Ladungsdichte” bedeuten. (Eingehende Betrachtungen hierzu sind in Vorbereitung.) Dies deutet auf ein Wirkvolumen der Teilchen hin, das die Kernkräfte und über die Atomradien letztendlich auch die gravitativen Kräfte nach außen hin regelt.
Zusätzlich unterstreicht dies alles noch einmal die erwähnte Dichteabhängigkeit der Gravitation. So wird z.B. eine massive Kugel von 1 kg (gewogen auf Erdradius) um 9.2 x10E-12 g stärker gravitieren als ihre beiden Hälften, diese jedoch im horizontalen Abstand von 1m gemeinsam gewogen.
Vorschau zu den Trägheitsbetrachtungen :
Über die Trägheit Wenden wir uns nun dem Problem zu, dass sich Massen mit einem noch näher zu bestimmenden Unwillen widersetzen, einer in irgendeine Richtung von außen auf sie wirkenden Kraft zu folgen. Sucht man die Ursache im Mach’schen Prinzip, wonach diese Erscheinung in der Kraftwirkung aller Massen des Universums auf die Probemasse zurückführbar ist, so impliziert dies einen Vergleich mit den Verhältnissen wie sie die Potentialtheorie beschreibt: Ein kugelförmiges Universum mit weitgehend homogen verteilten Massen übt wie eine Hohlkugelmasse auf eine irgendwo darin befindliche Probemasse keine Kraft aus.
Gleichwohl steht jede atomare Ladung mit allen anderen im Universum über die bekannte 1/R^2-Abhängigkeit in elektrischer Verbindung. Unter der Annahme eines (elektrisch kompensierten) universellen skalaren Feldes, gebildet durch die Summe aller Einzelladungsfeldlinien zwischen allen existierenden Atomen, muss nun beim von außen initiierten Verschieben eines Einzelatoms oder einer Masse in irgendeine Richtung des Universums die Länge aller ihrer atomaren Einzelladungsfeldlinien zu den in Bewegungsrichtung (= Vorwärtsrichtung) befindlichen Massen des Universums hin verkürzt, aber gleichzeitig(!) in den dazu inversen Richtungskoordinaten vergrößert werden, und nur diese Arbeit ist das Maß für die Trägheit. (Für alle Feldlinien der übrigen Raumwinkel rundum gilt das Gleiche unter Verrechnung der Richtungskomponenten.)
Ein etwa in Universumsmitte durch zusätzliche Krafteinwirkung von außen einmal beschleunigter Körper wird (ohne den Einfluss einer äußeren Störung in seiner Nähe) diesen vorerst gleichförmigen Bewegungszustand beibehalten wollen, und jede Veränderung dieses Zustandes ist mit einem weiteren ,,Hebevorgang” gegen das halbe Universum und einem gleichzeitigen ,,Fallen” hin zu seiner Gegenhälfte verbunden. Eine von außen hineingesteckte Hubarbeit (Beschleunigung) gegen das universelle elektrische Feld entspricht also augenblicklich einer gleichgroßen Fallenergie in die gleiche Richtung, die nur noch durch Abbremsung (Verzögerung) bei Kollision mit einer näherliegenden Störungsmasse in Wärme bzw. mechanische Deformation verwandelt werden kann.
(Im planetarischen Laborsystem entspräche dies dem Spezialfall der Beschleunigung waagerecht rollender Kugeln und deren Zusammenstoß. Für Drehbewegungen ergeben sich über Symmetriebetrachtungen vergleichbare Verhältnisse für das Abstandsquadrat des Trägheitsmomentes, jedoch verbleibt die Fallenergie als Drehimpuls in der betroffenen Masse. Demnach würden die Flieh- bzw. Trägheitskräfte rotierender Massen verschwinden, wenn das Universum ,,mitrotiert”.)
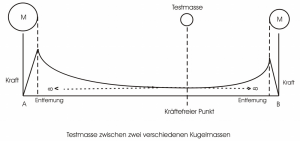
Generell bedeutet Bewegung in irgendeine Richtung also immer ein Fallen in Richtung eines Teiles des Universums, aber auch gleichzeitig ein Anheben gegen die Kräfte seines Restteiles. Bei Störung eines kräftefreien Punktes durch größere Massen oder bei Bewegung eines Probekörpers zwischen zwei Störmassen vom kräftefreien Punkt aus zwischen ihnen wird der differentielle Kraftzuwachs in Vorwärtsrichtung (= Fallen) deutlich stärker ansteigen als die Kraft des konstant gegen die Kraftlinienverlängerung wirkenden Teiles des Universums ( [dF/dx+ - dF/dx-] >> 0 ), und die Bewegung wird in Richtung des Zentrums der Störungsmasse weiter beschleunigt.
Eine gleichförmige Bewegung in Massennähe ist dann nur noch in tangentialer Richtung auf ihren Äquipotentiallinien möglich, in allen anderen Richtungen addiert sich die Wirkung der Störkraft lotwinkelabhängig zu den universellen Massenkräften, die wir als Trägheit wahrnehmen. Innerhalb des Universums erscheinen uns die Trägheitskräfte mangels fehlender Messgenauigkeit nach allen Richtungen gleich, werden jedoch durch Störmassen um uns herum verändert. Neuerdings ergaben Messungen von Gerschtein et al. am M.I.T. verschiedene Massenanziehungswerte, je nach Orientierung zu den Fixsternen, womit weitere Hinweise auf die hier gemachten Annahmen vorliegen.